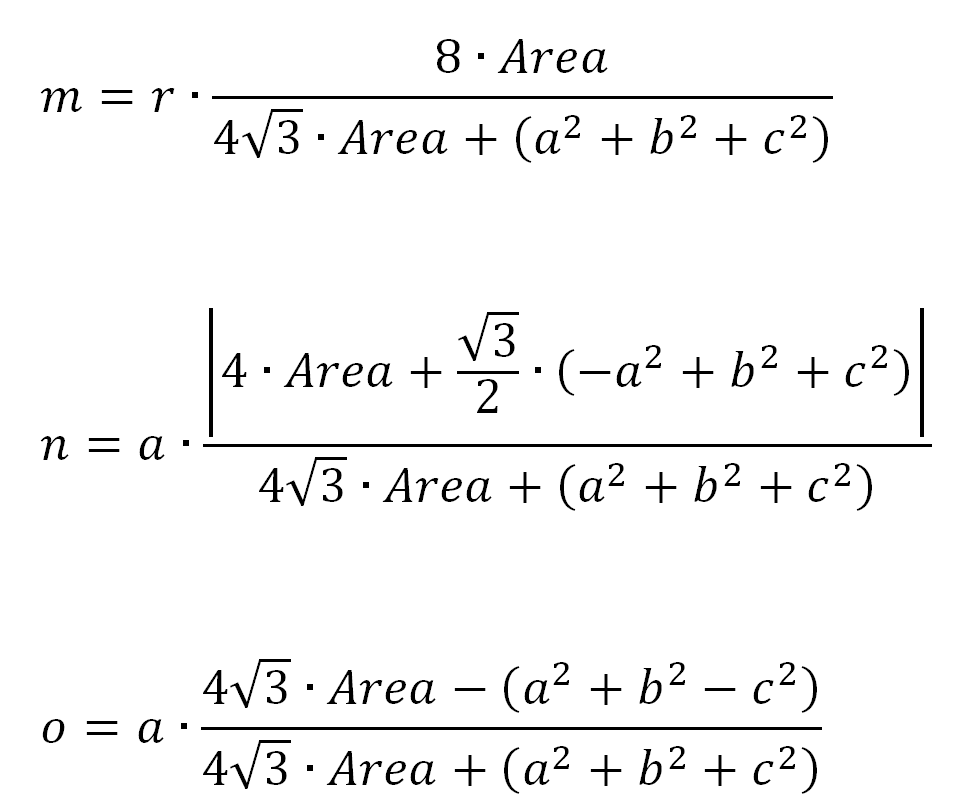What is OK Geometry?
OK Geometry is a tool for analysing dynamic geometric constructions. It generates reliable conjectures based on automated observation of dynamic constructions.Given a dynamic geometric construction, OK Geometry detects patterns, certain geometric properties of the construction, and algebraic relationships between geometric quanities. You can think of OK Geometry as of a pair of geometric spectacles for observing invariants of dynamic geometric constructions or as tool for generating conjectures. Observing and conjecturing are important processes, especially when proving facts.
OK Geometry also contains a prover. If successful, it produces a readable deductive proof.
More...
OK Geometry is freeware. The program can be used on three levels: Easy (for occasional users), Basic (for enthusiasts), and Plus (for experts in planar geometry). OK Geometry Easy and Basic are available in English, Czech, German, Italian and Slovenian.
Observing dynamic constructions
The Easy mode of OK Geometry allows simple observation of constructions created with different dynamic geometry systems (Cabri Geometre, Cabri Express, GeoGebra, Cinderella, Z.u.L. ( Zirkel und Linien), JGEX, Sketchometry, OK Geometry).Here is an illustration: Consider a square ABCD. Let E and F be the midpoints of CD and DA respectively, and let G and H be the intersections of CF with AE and CE respectively.

We show just a few of the several dozens of properties detected with OK Geometry.
Creating configurations
The Basic mode of OK Geometry is intended for the creation and observation of dynamic constructions. It differs from other dynamic geometry systems in that it includes some complex constructions (e.g. the construction of a circle tangent to three objects) and the creation of geometric configurations based on implicit constructions and optimization tasks.
Consider, for example, the following situation: For a given point P in a triangle ABC, you can construct three equilateral triangles having P as one of the vertex while the other two vertices lie on sidelines AB and BC, BC and CA, CA and AB. (You just rotate the triangle around P by 60 degrees.)
Is it possible to position P so that the three equilateral triangles are congruent? You can ask OK Geometry to position P so that this additional condition (congruences of the three equilateral triangles) is fullfilled. You can then use OK Geometry to obtain conjectures about the geometric properties of the point P and the resulting configuration.
Analysing triangles
The Plus mode of OK Geometry combines automated observation with a large database of characteristic triangle objects. The database consists of thousands of triangle centres (e.g. orthocentre), hundreds of lines (e.g. Euler line), circles (e.g. nine point circle), triangles (e.g. orhic triangle), conics (e.g. Kiepert hyperbola), transformations (e.g. isogonal conjugation). The objects from the database can be used both when creating constructions and when observing them.The figure illustrates part of the analysis of a configuration (three congruent equilateral triangles inscribed in a triangle as shown). OK Geometry conjectures that the common centre of the three triangles is the centre X15, i.e. the first isogonic centre of the triangle ABC. Moreover, the point under consideration appears to be related to some characteristic objects of the triangle ABC.
Advanced query of objects
 |
OK Geometry not only observes geometric properties among objects in a configuration, but also tries to relate objects to objects that are not part of the configuration. Consider, for example, the first isodinamic point P of the triangle ABC. The usual way of constructing the point P is via the three Apollonian circles. OK Geometry conjectures other constructions for P. It is a challange for the user to prove their correctness. |
Creating deductive proofs
OK Geometry is primarily intended for the observation of facts in plane geometry and the discovery of conjectures. However, since proofs are the essence of mathematics, OK Geometry is equipped with a mechanism for creating proofs of observed facts. The prover is based on the Geometry Deductive Database method and, if successful, generates a human-readable deductive proof.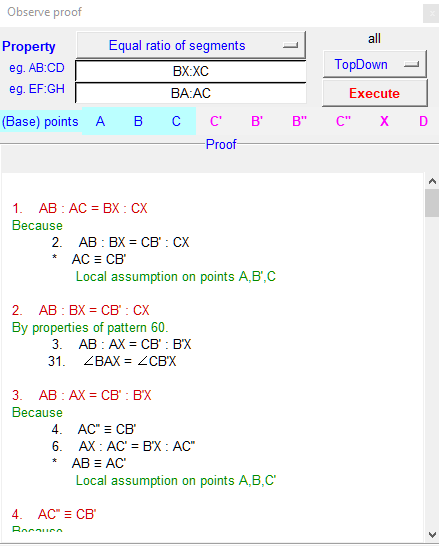
The correctness of the above proposed construction of the isodynamic point of a triangle can thus also be proven deductively. To enable the proof, OK Geometry added an auxiliary point to the construction and produced a proof.
Observing algebraic relationships
With OK Geometry you can also observe and conjecture algebraic relationships between geometric quantities in a dynamic construction.We illustrate this with an example: the isodynamic point P of a triangle ABC gives rise to three congruent triangles having two vertices on the sides of the triangle and P as the third vertex. Here are some conjectures obtained with OK Geometry about the length of the emphasised segments in this configuration.