Simple triangle analysis of objects
A simple method for identifying objects in a triangle
Simple triangle analysis is an observation technique in which the object under consideration (a point, line, circle or conic) is related to characteristic objects of a triangle, which is declared as the reference triangle. It uses a relatively large database of triangle objects.Simple triangle analysis can be invoked in the Sketch Editor with the command Special|Analyse object in reference triangle or using the △? button in the toolbar the right edge of the display. Before analysing one usually declares the reference triangle with the command Command|Set reference triangle. Then simply click in the displayed configuration on the object to be identified . A self-explanatory widget like the one shown below will appear.
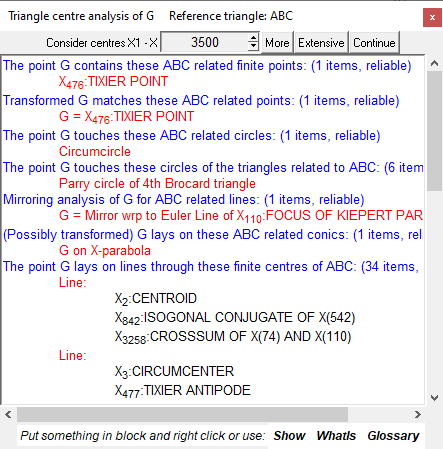
The widget may contain a lot of technical terms. To get the definition and explanation of a term, click on the Whatis command in the widget and then on the term in the information area of the widget. You can also display in the configuration one or more objects mentioned in the information widget: Just put them into a block and click the Show command in the widget.
Remember that the information obtained is a result of observation. The found relations can be very useful as hypothesis, but to fully rely on them, they must be proven.
We will illustrate the Simple triangle Analysis with a few examples.
Example 1

For a given triangle ABC let na, nb, nc be the images of the nine-point circle n of ABC in the sidelines of ABC. We consider the circle k, which is externally tangent to the circles na, nb, nc. In particular, we would like to obtain some information about the centre P of the circle k.
Creating the described configuration with OK Geometry, we declare the triangle ABC as the reference triangle, moreover we can create the nine-point circle with the command Special|Triangle derived object and the circle k with the command Circle|Circle 3 objects. Finally, we invoke the command Special|Analyse object in reference triangle and click on the point P.
Observation shows that the point P coincides with the Kosnita point (X54) of the triangle ABC. To learn more about the Kosnita point, we use the WhatIs command and click on the Kosnita point in the text. We obtain an illustrated explanation (definition): Let O be the circumcentre of a given triangle ABC and let A' be the centre of the circle through the points B, C, O. Define B' and C' cyclically. The lines AA', BB', CC' concur in a point P called the Kosnita point (X54) of the triangle ABC.
It can be proved that the observation about the point P is true. The fact that P is the Kosnita point of the triangle ABC makes it possible to construct the original configuration by the 'paper and pencil' method.
Analogous results are obtained for the centre of the circle that contains the circles na, nb, ny and is tangent to all of them.
It can be proved that the observation about the point P is true. The fact that P is the Kosnita point of the triangle ABC makes it possible to construct the original configuration by the 'paper and pencil' method.
Analogous results are obtained for the centre of the circle that contains the circles na, nb, ny and is tangent to all of them.

Example 2
For a given triangle, let pA be the radical axis of the nine-point circle n of ABC and the Apollonius circle kA of ABC through the vertex A. (That is, kA is the locus of points X for which |BX|:|CX| = |BA|:|CA|, and pA is the line through the intersections of kA and n. Define kB and kC cyclically.
The Observe command shows that that the lines pA, pB, and pC concur in a point M. We wonder what this point is.
The Observe command shows that that the lines pA, pB, and pC concur in a point M. We wonder what this point is.

Observation with Simple triangle analysis shows that the point M does not appear to be a known ETC centre. Here is an excerpt of the hypotheses we nevertheless obtain about M:
- M lays on the Brocard axis of the triangle ABC (i.e., on the line through the circumcentre X3 and the symmedian point X6 of ABC).
- M lays on the line through the centres X587 (i.e., the midpont of the centroid X2 and the symmedian point X6 of ABC) and the centre X1003 (i.e., the intercept of the Euler line and the line through X6 (symmedian point) and X99 (Steiner point) of the triangle ABC.
- M is the midpoint of the centres X574 and X5034 of ABC.
- M lays on the Fermat line of the orthocentroidal triangle of ABC.
- The isogonal conjugate of M lays on the Kiepert hyperbola of ABC.
- (etc.)
Example 3
In a given triangle ABC, let kA be the circle whose centre is on the side BC and which touches the sidelines AB and CA. Define kB and kC cyclically.Let k be the circle (if it exists) that is contained and is tangent to all three circles: kA, kB and kC.
The circle k can be created in OK Geometry Sketch Editor using the command Circle|Circle 3 objects. The Simple triangle analysis does not provide any valuable information about the centre of circle k.
The circle k can be created in OK Geometry Sketch Editor using the command Circle|Circle 3 objects. The Simple triangle analysis does not provide any valuable information about the centre of circle k.


The Special|Object analysis in reference triangle command reveals a surprising fact when applied to the circle k. The circle k is tangent to the nine-point circle of the intouch triangle of ABC. Thus, if A', B', C' are the points of contact of the incircle of ABC with the sidelines of ABC, then the circle k is tangent to the nine-point circle of A'B'C'. Let P be the point of contact of the two circles.

The observation also suggests that the circle k is tangent to the circumcircle of inverse-in-incircle triangle. In other words: If A'', B'', C'' are the respective inverses of the vertices A, B, C in the incircle of ABC, then k is tangent to the circumcircle of A''B''C''. This circle is, according to the observation, the same as the nine.point circle of the intouch triangle of ABC.
Downoload figures (.png)
Download examples (.p)