Observe properties of dynamic constructions

Even on simple geometric configurations OK Geometry detects (but does not prove) a variety of geometric properties.

To prove means to logically relate the given facts via intermediate facts to the consequence to be proved.  Being aware of the intermediate facts is therefore an important step in this process. OK Geometry is a tool for automated observation of dynamic constructions. Observations can be viewed as hypotheses and potential intermediate steps in a proof. It is up to the user to select the relevant hypotheses and combine them into a proof.

OK Geometry can observe dynamic constructions created with some of the popular dynamic geometry software (Cabri, Cabri Express, GeoGebra, Z.u.L, JGEX, Sketchometry, OK Geometry). It detects (but does not prove) a variety of properties, ranging from collinearity of points to harmonic quadruplets. It is possible to reduce the observations from the elementary ones to the advanced.

Observing a dynamic construction is quite simple: read the dynamic construction with the Task command and press the Observe command. A list of detected properties will appear. If you click on a property, its visual representation will appear. 

Example 1

In a right triangle ABC let D be the base of the altitude from the vertex C. Let E and F be the incentres of the triangles ADC and BDC respectively.


OK Geometry generates a list of the observed properties of the (dynamic) construction described above. The length of the list depends on the level of analysis. Note that some of the listed properties are trivial (e.g. the points A, D, B are collinear), others are not. 



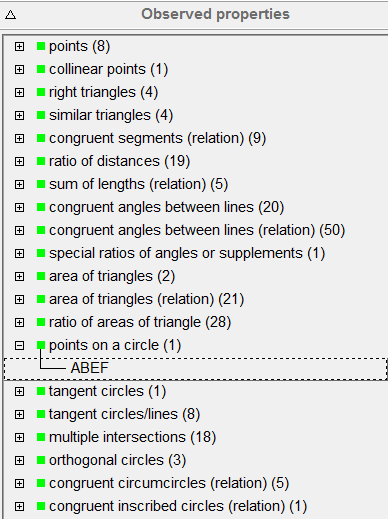
For example, one may not be aware that the points A, E, F, B lay on the same circle.

Example 2

In a right triangle ABC, let D be the midpoint of BC and let E be the base of the altitude at C in triangle ACD. 
Prove that the triangle EBD is similar to the triangle BAD.
Proving the similarity of triangles EBD and BAD is probably not a trivial task for high school students. OK Geometry observes several properties of the above configuration. One of them is shown below: The circles through AEB and through DEB intersect on the hypothenuse AB. Considering this property and the intersection point can pave the way to the proof for the similarity of triangles EBD and BAD. 


Download figures (png)

Download constructions (p)