Observe algebraic relationships
Observe polynomial relations between geometric quantities
With OK Geometry, you can observe polynomial relationships between geometric quantities (distances, perimeters, areas, etc.) in dynamic constructions. You can also observe the ratio of two quantities and express it as a rational function. Such observation can provide valuable hypotheses, but does not prove them.
Observation of algebraic expressions is accessible on the menu command Commands|Observe formulae. Details on this command and its use can be found in the OK Geometry Plus Reference manual. The Observe formulae command has three variants:
- Simple. The simple variant observes polynomial relationships between variables obtained by direct measuring in OK Geometry. For example: investigate a possible relationship between the sides and the diagonals of a deltoid (kite).
- Advanced. This variant relates a specified variable or ratio of variables to selected geometric quantities. For example: How to express the area of a triangle in terms of the lengths of its three medians?
- Triangle. This variant allows you to express a variable or a ratio of parameters with commonly used quantities of a reference triangle. The reference triangle must be a general triangle, that has no specific properties. For example: find an expression for the length of a median in a triangle.
- Obtain a dynamic construction of the considered configuration.
- Measure or calculate the geometric quantities to be considered. The Simple option requires that all quantities be measured directly. For the Triangle option, specify only one quantity or a ratio of quantities. For the Triangle option and the Advanced option, the quantities can be parameters obtained by measurement or calculation, but they can also be described with a simple syntax. The names of the quantities should begin with a lowercase letter for 1-dimensional quantities and an uppercase letter for 2-dimansional quantities.
- Fill in the form of the command. In addition to entering the names of the quantities/parameters, you can optionally include transformations (of quantities) and the strength of the observation. Especially in Triangle option, both can significanly affect the computation time.
- Click on the Observe button in the form. The software may detect one, several or no relationship. A detected relation can be directly included (as a Boolean parameter) into the construction, so you can additionally check it by dragging.
- The obtained results usually require some algebraic manipulations, depending on your needs and taste.
Example 1. Simple case
In the figure, points A, C, D are collinear, BC is orthogonal to AD, and |AD|=|AB|. The small circle is tangent to the line BC, the line AC and the circle k(A,B). We have measured the radius r of the small circle, and the lengths v, u, t of the sides of the triangle ABC. Our goal is to relate the radius r to the side lengths of the triangle ABC.
In the Simple option, we select, which quantities to consider. The observation then looks for the simplest relationship between them.
If we select all four quantities t,u,v,r, the observed relationship will be u2 + v2 = t2 . Probably this is not the type of relationship we are looking for.
If we select the quantities t,u,r , the observation will yield a result "Nothing found", because there is no (simple) polynomial relationship between these quantities.
Selecting the quantities u,v,r, gives the result:
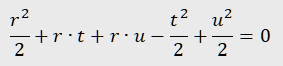
Proving the result is a nice high school task. From the expression we obtain
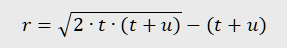
In the Simple option, we select, which quantities to consider. The observation then looks for the simplest relationship between them.
If we select all four quantities t,u,v,r, the observed relationship will be u2 + v2 = t2 . Probably this is not the type of relationship we are looking for.
If we select the quantities t,u,r , the observation will yield a result "Nothing found", because there is no (simple) polynomial relationship between these quantities.
Selecting the quantities u,v,r, gives the result:
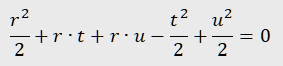
Proving the result is a nice high school task. From the expression we obtain
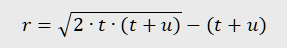

Example 2. Triangle case

Let A' be the point of contact of the incircle of a given triangle ABC with side BC. Find the radius ra of the circle that lays on the side of BC opposite from A, touches the side BC of the triangle at A', and also touches the circumcircle of ABC.
We first obtain a configuration and declare the measured radius of the considered circle as parameter ra. The Triangle version of the Formulae observation (with default settings) gives several expressions for the parameter ra. The first one is
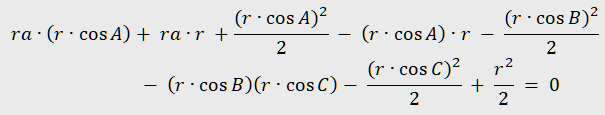
where r is the radius of the circumcircle of the reference triangle ABC. A manipulation of this expression gives
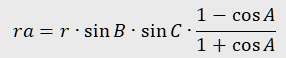
Another expression from the observation results involves the radius ri of the inscribed circle in the reference triangle ABC:
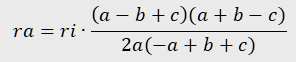
Example 3. Triangle observation
Continuing the previous example, we show how to obtain the trilinear coordinates of a point with respect to a reference triangle. If A', B', C' are the points of contact of the sides of the triangle ABC with its incircle, then it follows easily from Ceva's theorem, that the lines AA', BB', CC' concur in a point G, which is the Gergonne point of the triangle ABC.
We use the predefined notation xt(G) for the oriented distance between the point G and the sideline BC. The values yt(G) and zt(G) are defined cyclically. The position of the point G is described by the ratios xt(G) : yt(G) : zt(G). The expressions for xt(G), yt(G), zt(G) are often difficult to obtain, so we do the observation for the ratios, e.g. yt(G) : zt(G).
In our case, observing the ratio yt(G) : zt(G) yields several expressions :
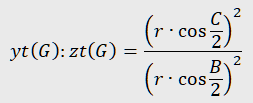
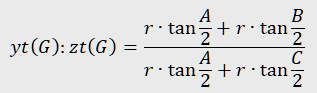
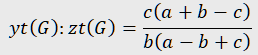
From the second expression, for example, we can deduce the trilinears for the Gergonne point of the triangle:
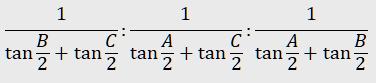
We use the predefined notation xt(G) for the oriented distance between the point G and the sideline BC. The values yt(G) and zt(G) are defined cyclically. The position of the point G is described by the ratios xt(G) : yt(G) : zt(G). The expressions for xt(G), yt(G), zt(G) are often difficult to obtain, so we do the observation for the ratios, e.g. yt(G) : zt(G).
In our case, observing the ratio yt(G) : zt(G) yields several expressions :
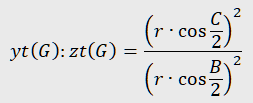
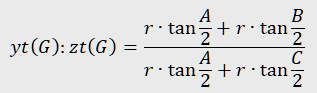
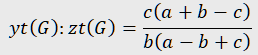
From the second expression, for example, we can deduce the trilinears for the Gergonne point of the triangle:
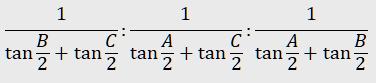

Example 4. Advanced Formulae observation

We consider a generalisation of Example 2.
For a given triangle ABC, find the radius u of a circle laying on the side of BC opposite from A, touching the side BC of at a given point D and touching the circumcircle of ABC.
The Advanced option requires the specification of variables used in the expression for the radius u. Besides the distances p = |BD| and q = |CD| the value u is determined by the radius r of the circumcircle of ABC and/or the size of angle A. Angles cannot be treated as variables so we can use predefined 1-dimensional entities, e.g., cA = r·cos(A), sA2 = r·sin(A/2).
For example, a good choice of variables for u is, for example, p, q, r, cA. The observation gives
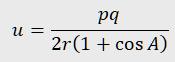
Proving this relation is a nice challenge.
For a given triangle ABC, find the radius u of a circle laying on the side of BC opposite from A, touching the side BC of at a given point D and touching the circumcircle of ABC.
The Advanced option requires the specification of variables used in the expression for the radius u. Besides the distances p = |BD| and q = |CD| the value u is determined by the radius r of the circumcircle of ABC and/or the size of angle A. Angles cannot be treated as variables so we can use predefined 1-dimensional entities, e.g., cA = r·cos(A), sA2 = r·sin(A/2).
For example, a good choice of variables for u is, for example, p, q, r, cA. The observation gives
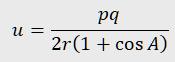
Proving this relation is a nice challenge.
Example 5. A final example

In the figure, each vertex of the triangle ABC is projected orthogonally onto the opposite side and from there separately onto the two adjacent sides. It turns out that the resulting 6 points lay on the same circle, called the Taylor circle of the triangle ABC. You can use the Triangle variant of Formulae observation to find out how is the radius t of this circle related to the standard parameters of the triangle. Here is an elaboration of the observation:
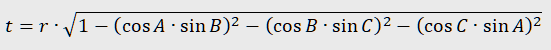
Download figures (png)
Download constructions (p)